Chain (or belt) & sprocket wear influences: 'Same tooth - same link' situation
 

'Same tooth - same link' situation
This happens when the number of links of the chain divided by the number of teeth on a sprocket is a round number. Let's assume you have a chain with 60 links, a front sprocket with 10 teeth and a rear sprocket with 20 teeth.
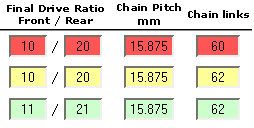
(F = 10, R =20 L = 60) Not a very realistic situation but easier for the example.

The number of Links divided by teeth on Front = L / F  = 60 /10 = 6
This means that after six rotations of the front sprocket, the chain made exactly 1 rotation and the first tooth on the front sprocket hits the exact same link of the chain.

Same goes for the rear: L/R= 60/20=3. So every 3 rotations of the rear sprocket, the chain made 1 complete rotation and the teeth are exactly in the same position again.
So when this chain rotates once, both front and rear sprockets are in the same position and hit the same link all the time. This is not good.

It would be better if the chain had un uneven number of links, say 61. Since this is not very likely (chains almost always have an even number of links), lets take a chain with 62 links. The calculation now are:

Front: L/F = 62/10 = 6.2
Rear:  L/R = 62/20 = 3.1

This means that after 1 rotation of the chain, the front made 6.2 and the rear 3.1 rotations. This means other teeth hit the same link in the chain ! That is better !

Now how long (how many rotations of the chain) does it take this time for the teeth to hit the same link again? We then have to find the out how many links will have to pass before the division results in an even number. That is the case when we have the LCD of these numbers, the Least Common Multiple. This can be calculated using the GCD, the Greatest Common Denominator. The GCD for 62 and 10 is 2, that is the greatest number both can be dived by which results in an even number.
Now the LCD = the multiple of 62 and 10 divided by the GCD:  (62 * 10)/2 =  310.
this means after 310 links, the front sprocket is in the exact same position again.
310 links means 310 / 62 =  5 rotations of the chain. So when having a china with 62 links instead of 60 links, results in less wear because now only every 5 rotations of the chain, the same tooth is hit.

So what would be the optimum number of chain rotations then ? That would be when we have a maximum number of links needed for the same position. So the division LCD = (#1 * #2) / GCD should be maximum. That is the case when GCD = 1 cause the result would then be (#1 * #2) / 1 = #1 * #2.
So when the GCD is 1 we reached our goal. This happens when one of the number is uneven. Lets say we take an 11 sprocket instead of a 10 sprocket, Rear =20 and Links = 60. This results in a GCD of 1 and the number of links needed is: (11 * 60) / 1 = 660 links. This means the chain has to rotate 660/60 =  11 times before the same tooth hits the same link again. This is the optimum !

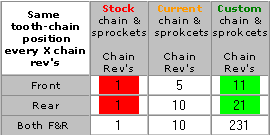
So what the relative chain wear indicator 'Same tooth - same link'  table does, is showing the number of chain rotations it takes with selected number of teeth and links to hit the same tooth-link combination and also marks them.

• The Worst is of course 1 rotation (background marked red) when every rotation of the chain all teeth hit the same link all the time.

• The Optimal combination (background marked green) is when the chain has to rotate "the number of teeth on the sprocket" to hit the same tooth again.

In general, the more chain rotations it takes to hit the same tooth-link or link-tooth combination, the better.
This way you can check if your chosen sprockets and chain are a better or worse combination than to one you have or was stock. So it is relative compared to the other combination, it is not an absolute indication for chain wear.

Next: Number of tooth-link contacts